... MAIS ON VA LE FAIRE !!!
- PRODUIT DE MATRICES
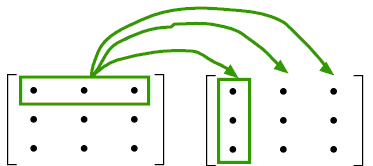
UNE MATRICE = LISTE DE SES LIGNES
|
(DEFINE (EXPONENTIELLE X N)
(COND ((= N 1) X)
(ELSE (* X (EXPONENTIELLE X (- N 1)))
(ODD? N) = LE CONTRAIRE
|
(DEFINE (EXPO-RAPIDE X N) (COND ((= N 1) X)
((EVEN? N) (EXPO-RAPIDE (* X X) (/ N 2))) |
(TIME EXP)
--> AFFICHE LE TEMPS D'ÉVALUATION DE EXP, ET RENVOIE LE RÉSULTAT
TEMPS EXPRIMÉ EN MILLIÈMES DE SECONDES
AFFICHE 3 VALEURS :
cpu time: 1800 real time: 1800 gc time: 0
--> CALCUL = 1,8 seconde
(DEFINE (AFFICHE-TEMPS X N1 N2)
(DISPLAY "n=") (DISPLAY N1) (NEWLINE)
(DISPLAY "rapide=") (TIME (EXPO-RAPIDE X N1)
(DISPLAY "normal=") (TIME (EXPONENTIELLE X N1)
(IF (> N1 N2) 'STOP
(AFFICHE-TEMPS X (+ N1 10) N2)))
... ET SI ON L'APPLIQUAIT À DES MATRICES ?
--> IL SUFFIT DE REMPLACER LE PRODUIT DE NOMBRES * PAR LE PRODUIT DE MATRICES : MAT*MAT
(DEFINE (EXPO-RAPIDE X N)
(COND ((= N 1) X)
((EVEN? N)
(EXPO-RAPIDE (MAT*MAT X X) (/ N 2)))
(ELSE (MAT*MAT X (EXPO-RAPIDE X (- N 1)))
... MAIS ON VA LE FAIRE !!!

UNE MATRICE = LISTE DE SES LIGNES
(DEFINE (MAT*MAT M1 M2)
(COND ((NULL? M1) '())
(ELSE (CONS (LIGNE*MAT (CAR M1) M2)
(MAT*MAT (CDR M1) M2)))))
(LIGNE*MAT L M) ? = PRODUIT DE LA LIGNE L PAR TOUTES LES COLONNES DE M
(DEFINE (LIGNE*MAT L M)
(COND ((VIDE-COL? M) '())
(ELSE (CONS (LIGNE*COL L (PREMIERE-COL M))
(LIGNE*MAT L (RESTE-COL M))))))
(DEFINE (LIGNE*COL L C)
(COND ((NULL? L) 0)
(ELSE (+ (* (CAR L) (CAR C))
(LIGNE*COL (CDR L) (CDR C))))))
(PREMIERE-COL M) = PREND LE PREMIER ÉLÉMENT DE CHAQUE LIGNE DE M --> APPLIQUE CAR À CHAQUE LIGNE
(DEFINE (PREMIERE-COL M) (MAP CAR M))(DEFINE (RESTE-COL M) (MAP CDR M))
(DEFINE (VIDE-COL? M) (NULL? (CAR M)))