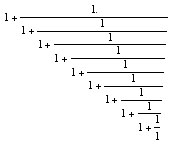
Taper des expressions diverses.
Calculer l'expression suivante pour x = 1, puis chercher x donnant la valeur la plus proche de pi :
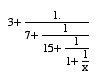
Scheme - TD n° 1
13 février 2002
Expressions numériques
1 + 2*(4 - 7/5)
cos2x + sin2x
racine(1 + racine(2 + racine(3 + x)))
Indiquer quelles sont les expressions correctes et leur résultat :
Welcome to DrScheme, version 101. Language: Graphical Full Scheme (MrEd). > (+ -3 (- -3) (- 3)) -3 > (- (+ 1 2 (- 3 (+ 1 2)))) -3 > (- (+ 1 - (3 (+ 1 2)))) procedure application: expected procedure, given: 3; arguments were: 3 > (- (+ 1 - (+ 1 2))) +: expects type <number> as 2nd argument, given: #<primitive:->; other arguments were: 1 3 > (+ (sqrt (sqrt (- 20 4)))) 2 > (- 20 (sqrt (sqrt (4)))) procedure application: expected procedure, given: 4 (no arguments) > (+ 2 3 (sqrt 2 3 (- 2 3))) sqrt: expects 1 argument, given 3: 2 3 -1Donner les réponses de Scheme :
> (define x 3) > (+ x (* 2 x)) 9 > (define x (* 2 x)) > (+ x (* 2 x)) 18 > (define y (* 3 x)) > (define x (* 3 y)) > (+ x (* 2 x)) 162 > (+ y (* 2 y)) 54 > (let ((x y) (y x)) (+ x y)) 72Définir en Scheme les fonctions :
f(x) = racine(1 + racine(2 + racine(3 + x)))
g(x) = racine(1 + racine(2 + racine(3 + racine(4 + racine(5 + racine(6 + x))))))
Définir en Scheme la fonction :
f(x) = 1 + racine(3 + 7/x) + log(1 + racine(3 + 7/2x) - 4)
Calculer l'expression suivante pour x = 1, puis chercher x donnant la valeur la plus proche de pi :
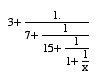
Welcome to DrScheme, version 101.
Language: Intermediate Student.
> (define (f x y) (+ x (/ 1. y)))
> (define (approx x) (f 3 (f 7 (f 15 (f 1 x)))))
> (approx 1)
#i3.141552511415525
> pi
#i3.141592653589793
> (approx 292)
#i3.1415926530119025
> (approx 293)
#i3.141592653921421
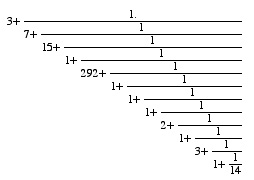
Les décimales suivantes de pi étant 3.14159265358979, on peut continuer la construction précédente. Faire (suivant x) calculant 1/decimale(x), et utiliser suivant pour retrouver le développement de pi : 3, 7, 15, 1, 292, etc.
> (define (suivant x) (/ 1 (- x (truncate x)))) > (define x1 (suivant pi)) > x1 #i7.062513305931052 > (define x2 (suivant x1)) > x2 #i15.996594406684103Calculer le développement du nombre exponentiel e et du nombre d'or : (1+racine(5))/2. Vérifier que la fraction obtenue est une bonne approximation.
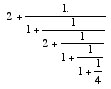
> e #i2.718281828459045 > (define z1 (suivant e)) > z1 #i1.3922111911773332 > (define z2 (suivant z1)) > z2 #i2.549646778303843 > (define z3 (suivant z2)) > z3 #i1.8193502435980868 > (define z4 (suivant z3)) > z3 #i1.8193502435980868 > (define z5 (suivant z4)) > z5 #i4.535573476086956 > (f 2 (f 1 (f 2 (f 1 (f 1 4))))) #i2.71875 > e #i2.718281828459045
> (define n (/ (+ 1 (sqrt 5)) 2.)) > n #i1.618033988749895 > (define y1 (suivant n)) > y1 #i1.6180339887498947 > (define y2 (suivant y1)) > y2 #i1.6180339887498953 > (define y3 (suivant y2)) > y3 #i1.6180339887498936 > (define y4 (suivant y3)) > y4 #i1.6180339887498982 > (define y5 (suivant y4)) > y5 #i1.618033988749886 > (define y6 (suivant y5)) > y6 #i1.618033988749918 > (define y7 (suivant y6)) > y7 #i1.6180339887498343 > (define y8 (suivant y7)) > y8 #i1.6180339887500534 > (f 1 (f 1 (f 1 (f 1 (f 1 (f 1 (f 1 (f 1 (f 1 1))))))))) #i1.6181818181818182 > n #i1.618033988749895