Scheme
Scheme - TD n° 2
6 mars 2003
Expressions conditionnelles, car, cdr
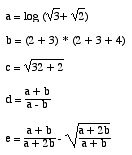
(define a (log (+ (sqrt 3) (sqrt 2))))
(define b (* (+ 2 3) (+ 2 3 4)))
(define c (sqrt (+ (expt 3 2) 2)))
(define d (/ (+ a b) (- a b)))
(define e (let ((x (/ (+ a b) (+ a b b))))
(- x (sqrt (/ 1 x))))
Ecrire en Scheme l'expression calculant :
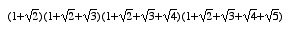
(let ((a (sqrt 2)) (b (sqrt 3)) (c (sqrt 5)))
(* (+ 1 a) (+ 1 a b) (+ 1 a b 2) (+ 1 a b 2 d)))
(let* ((a (+ 1 (sqrt 2))) (b (+ a (sqrt 3)))
(c (+ b 2)) (d (+ c (sqrt 5))))
(* a b c d))
Donner les réponses de Scheme :
> (or (> 1 2) (< 1 2)) #t > (and (> 1 2) (< 1 2)) #f > (not (not (> 1 2))) #f > (and (not #f) (not #t)) #f > (and () 2) 2 > (and 3 4 2) 2 > (or 5 3 1) 5Donner les réponses de Scheme :
> (if #t #t #t) #t > (if #f #f #f) #f > (if #t #f #t) #f > (if #f #f #t) #tDonner les réponses de Scheme :
> (and #t a) reference to undefined identifier: a > (and #f a) #t > (or #t a) #t > (or #f a) reference to undefined identifier: aDonner les réponses de Scheme :
> (define l (list 1 2 3 4 5 6)) > (car l) 1 > (cdr l) (2 3 4 5 6) > (car (cdr l)) 2 > (list (car l) (car (cdr (cdr l)))) (2 4) > (list (car l) (cdr l)) (1 (2 3 4 5 6))Donner les réponses de Scheme :
> (define l (cons (list 1 2) (list 3 4))) > (car (cdr l)) 3 > (cdr (car l)) (2) > (cons 1 (cdr l)) (1 3 4) > (list (cdr (cdr l)) (car (car l))) ((4) 1)Donner les réponses de Scheme :
> (define l (cons #f (list (> 4 5)))) > (cons #t (cdr (cdr l))) (#t) > (list (cdr l) (car l)) ((#f) #f) > (if (car l) 0 1) 1 > (if (cdr l) 0 1) 0
(define (max3 a b c)
(plus-grand a (plus-grand b c)))
(define (plus-grand x y) (if (>= x y) x y))
(define (max4 a b c d) (plus-grand a (max3 b c d)))
; nombre quelconque d'arguments:
(define (maxn x . suite)
(if (null? suite) x
(plus-grand x (apply maxn suite))))
Scheme